HOW WELL ARE INDIAN
CHILDREN EDUCATED?

Chapter Four
RESULTS ON STANDARDIZED TESTS

Two types of tests were used in both 1945 and 1946. The data from the standardized examinations will be discussed in this chapter. Chapter 5 will analyze the data from the tests constructed especially for the Indian Education Evaluation Program.

Most of the graphs presented in this monograph are copies of the eighth grade norm sheets prepared for the 1945 study, upon which have been indicated the medians for the fourth and twelfth grade students, who took the same tests in 1946. Only part of the original norm sheets have been duplicated in this monograph, but the medians and quartiles computed for all distributions and all tests are given in Tables 1 and 2, Appendix F.

Attention should be drawn to several things in studying the norm sheets. It will be noted from the numbers at the bottom of each graph, that some distributions are based upon a large number of cases whereas others are based upon only a few. In those instances in which there were only a few cases one must be cautious in drawing conclusions because the various statistics, such as median, quartiles and the like, cannot be interpreted as possessing the same degree of accuracy as those statistics based upon, larger samples. For example, fewer than 30 cases are used as a basis for the data describing the eighth grade Indian students in the Pacific area. This means that, though the median truly represents the mid-score or central tendency for this particular group of students, it cannot be depended upon as a highly accurate estimate of the kind of work that should be predicted of all eighth grade Indian students in the Pacific area. In most instances data were obtained from all of the fourth, eighth, of twelfth grade students enrolled in Indian schools. The charts therefore describe the actual status and performance in the schools in each area. It should be borne in mind that the size of the group tested determines the accuracy of predictions. These norms and distributions are intended to present a picture of the level of work being done by students in these different regions and types of schools. Their representativeness and accuracy are indicated by the figures which show the number of students tested. The number of students in a particular group or region may in itself be indicative of the uniqueness of the group. For example, a small number of students in Federal Indian schools in a particular region may indicate that Indian schools provide only for a particular type of student.

In the left-hand margin of each norm sheet a space was left in which the school might inscribe its own distribution of scores. The distributions are broken into four parts or quarters, each one representing the range of scores for one-fourth of the class or group. It will be observed that these distributions thereby have parts which may be described as lower or first quarter, second quarter, third quarter and upper quarter. The median is described as the score which is exceeded by fifty percent of the class. The median is the measure commonly used in computing test norms, because it is less affected by a few extreme scores and therefore more truly represents what most people would consider to be the central trend or tendency of the entire group.

The first six columns of each graph show for a specific test the distribution of scores in the types of schools studied. The classification of "school experience" or "type of school attended," assigned to each student, was on the basis of the type or types of schools in which he had received a significant amount of his training. It was at one time considered practical to develop norms and compute medians on the basis of the school which the students were attending at the time of testing. This would have meant, for example, that the norms established for boarding schools would have been based upon scores obtained by all eighth grade students enrolled in boarding schools in 1945. However, many eighth grade students in some boarding schools had only recently come to this type of school, having had a major proportion of their training in some other type of institution. It was decided that it would be better to derive norms for the boarding schools from the scores of students who had spent a significant amount of their time in boarding schools. For this reason it was necessary to identify the pupils by the type or types of schools in which they had received a significant amount of training and to prepare norms based upon these classifications.

It was then necessary to decide what should be considered "a significant amount of training." Sample distributions were made of scores of those students who had spent varying amounts of time in a certain type of school, but there were no sharp breaks which would give a clue as to what amount of time would be considered significant. As a matter of fact, there are undoubtedly so many variables in addition to length of time and type of school that one probably should not expect to find any simple means of justifying the establishment of a criterion number of years. It seemed evident from the types of examinations that were being required that many of these tests called for information and understanding that would have been accumulated and added to, over a great many years of schooling. This is particularly true in the case of arithmetic, reading and English. It is also true that the home economics, health and safety examinations, and some parts of the resources, were a kind in which the information could have been gathered almost exclusively during the seventh and eighth grades. It was finally concluded that a student who had spent three or more of his recent years in a single type of school should have his grades recorded and reported as belonging to that type of school. In other words, the student who had spent only one or two years in the type of school in which he was then a student, had had up to six years of training in another type of school or schools, and therefore it is difficult to attribute the degree of success he achieved in the examinations to any single type of school. An attempt was made to break the data down and demonstrate the achievement of students having had their training divided between two types of schools. This was not practical because the group for most combinations was far too small to warrant drawing reliable conclusions and also it is difficult, if not impossible, to tell how many years of early training are equivalent to two or three recent years. Those having received at least two years in Indian schools were grouped together under the heading of "Miscellaneous Indian" (schools). The relatively small numbers in the non-reservation boarding school groups at the fourth and eighth grade levels and the large numbers classified under Miscellaneous Indian are associated with the fact that many students enter non-reservation boarding schools already having attended school elsewhere. This is particularly true in such non-reservation schools as Sherman Institute, which has no grades below the seventh and therefore, it could have no eighth grade students who had been regularly promoted with three years in this school.

The remaining columns in each graph describe the distribution of scores in Indian schools in each of the regions studied and on the test indicated. In the 1945 study, it will be noted that all of the Southwest schools were considered as a group, whereas in the 1946 study this group was divided into Navajo, Pueblo and other Southwest. The Alaskan schools were included in the survey for the first time in 1946. Although tests were administered to a fairly large number of students in the Alaskan schools, only a relatively small number of students could be included in the sample from this area, because much of the necessary background information could not be obtained.

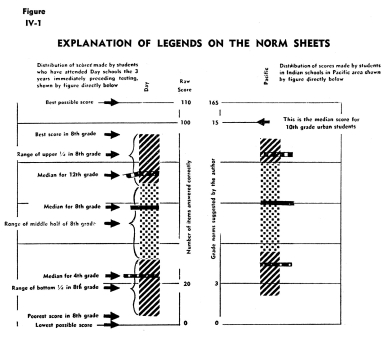
Figure IV-1 explains the legends on the various norm sheets, or graphs, included in this study. Except for the Gates Advanced Primary Reading tests, which are fourth grade tests, and the Free Writing Test, all of the plotted distributions describe the achievement of the eighth grade students. With the exception of the "Total Score" of the General Resources, the eighth grade distributions describe the 1945 results. The eighth grade distributions on the General Resources test describe the 1946 results, since the original test was extended and administered to both eighth and twelfth grade students in 1946. It should be noted that the lines drawn connecting the medians for each grade are to assist the reader in observing the differences between schools and areas, and that intermediate points on these connecting lines have no signficance.

On the graphs for the standardized tests the age or grade norms supplied by the test author have been inscribed on the graph. The norms as reported by the test publishers are not suggested standards for Indian and rural white student populations described here, but are indicated only because they do provide a yard stick which is in somewhat familiar terms. In other words, a grade difference of one grade equivalent means more to the average reader than a difference in raw score of "6 points" on some unknown scale.

Reading Ability

The data first listed describes the results on the Gates Reading Test. All four forms of this examination were given for the purpose of revealing analytically the difficulties, as well as the skills, of the different groups of students. There are some differences between the profiles of the four different forms of the Gates test. The eighth grade students of the non-reservation and public schools and students in Indian schools of the Mountain area rather consistently demonstrated a relatively high level of achievement on all four of these tests. The eighth grade Indian students in the Southwest were lowest on all four forms. In the case of Form C, the form designed to measure a pupil's ability to understand precise directions, students in Indian schools in the Lake States, Oklahoma and Pacific areas, do about as well, if not better than those in the Mountain area. It is interesting to note that the training represented by Miscellaneous Indian Combinations, which includes students who have been in two or more different types of Indian schools, do almost equally as well in these four types of reading abilities as do other Indian students. Only in Form B, that section measuring the prediction of outcomes, do these students with mixed training show any tendency to perform below the general average.

In form A of the Gates Basic Reading Test there appears to be a significant growth between the eighth and twelfth grade levels, with marked differences between the twelfth grade groups of the various types of schools and in the various areas. However, in Form B, on Predicting the Outcome of Given Events, there is much less difference between the achievement of the students in the various twelfth grade groupings. This may be due to a ceiling effect of the test itself, with the good students unable to show themselves superior to those of average ability. Because of the fact that there were only twelve twelfth grade students in the day schools in the entire Indian Service, in 1946, norms are not shown for this group.

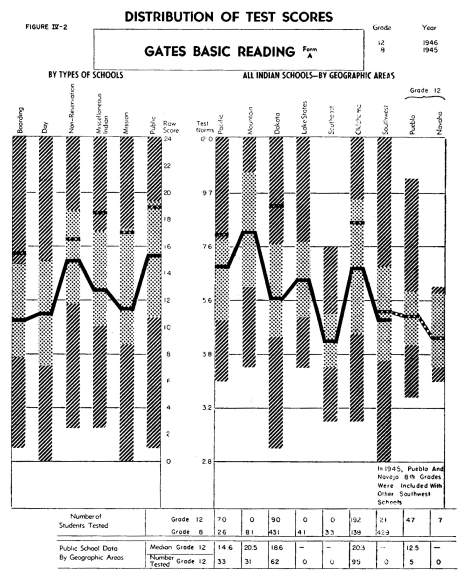
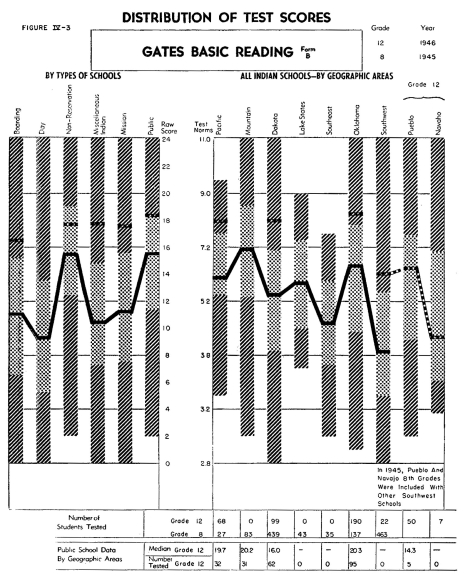
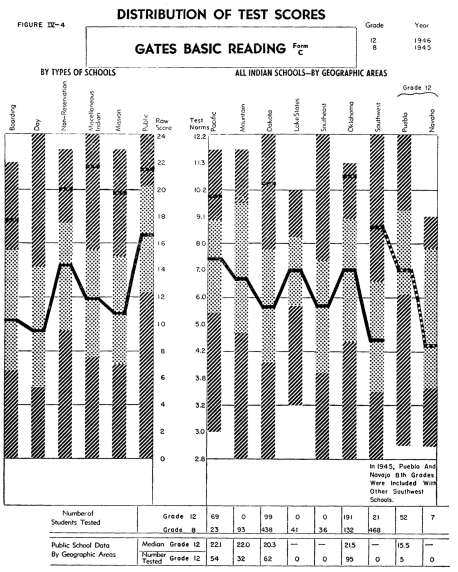
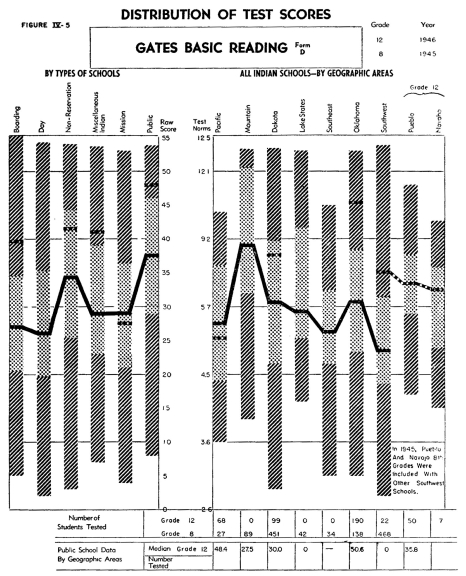
It is interesting that the Indian students often do as well or better than the public school students in those regions where relatively few Indian students attend the public schools. Differences between the achievement of the pupils in different regions may not indicate superior instruction and educational facilities in the one, but instead inequalities in the two school populations.

It is important to point out that small deviations between the medians are not, in most cases, statistically significant, or in other words, differences of this small magnitude may occur by mere chance. As an example, on Form B of the Gates Reading Test, it may be safe to assume that the non-reservation eighth grade group, with its median of about 15, shows a significantly higher level of achievement than the group of Indians in the Southwest with their median of about 8.5. However, while the chart shows that the Dakota Indians have slightly lower scores than the Lake States area, this small difference is probably due to mere chance.

The "National Norm Equivalents" have not been provided with the idea of suggesting any levels of attainment that are expected. National norms are commonly based upon either urban school children or, in some cases, a combination of urban and near-urban education. In view of this, it is obvious that national norms would not be the proper yardstick to use as a means of measuring or comparing achievement in this Indian education study. It should be repeated here that the students tested in the Indian evaluation study all come from a rural background and were taught in schools having a rural environment, and therefore these students should not be compared with the urban students, whose environment and curriculum are recognized to be quite different. The national norms do help to provide some concept of the range of abilities, and they also give one an understanding of the increments between grade levels in the urban school population. The national norms show the achievement of the rural students to be, in some instances, much higher than one might expect.

Figure IV-6 describes the achievement of the fourth grade students on the Gates Advanced Primary Reading Test, Type I, which is a measure of general reading vocabulary. While there is considerable variation in the median achievement recorded for the various groups, the range of these medians is only about the equivalent of one school year on the national urban type norms. While the range of the student scores within each of the groups is extremely large, varying in most cases from near zero to nearly 100% correct responses, yet the range of the middle 50% of the students within each group is quite similar for each of the types of schools and areas, namely a range of only a little more than one school year.

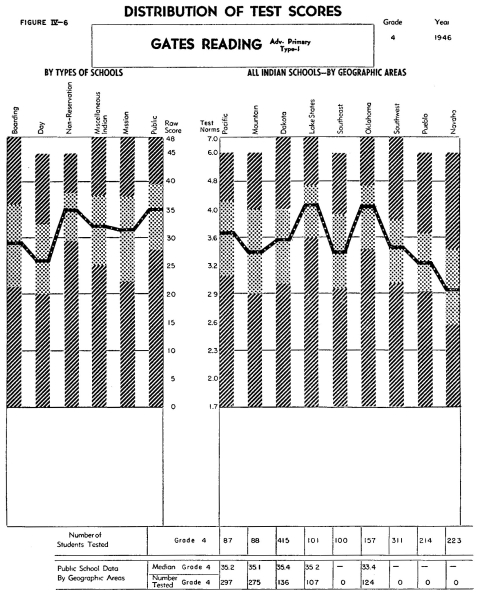
The reading vocabulary skill of the rural public school students appears to be about the some as that of the urban fourth grade students and the reading vocabulary achievement of the Indian students, while equal to that of the public school children in the Lake States, Oklahoma and Alaskan regions, in no case falls lower than the third grade urban levels. The fact that both urban and non-urban students at this level employ about the same basic reading vocabulary is probably the reason that the deviations from the urban norms are smaller here than at the eighth and twelfth grade levels. When one observes, on many of the tests given to the eighth and twelfth grade students, that the achievement of the Indian students was as much as two years below that of the national urban norms, one may be tempted to interpret this as a failure on the part of the instruction between the fourth and twelfth grade levels in the Indian schools. This may not be due entirely to instructional lack, or deficiency, but to any or all of the following factors:

1) the students now being tested in the eighth and twelfth grades probably do not represent the same type of student now found in the fourth grade, or, in other words, four years from now the eighth grade may be made up of students with a higher potential ability than those now attending eighth grade.

2) for students at the eighth and twelfth grade levels, the national norm yardstick may not be an adequate means of comparing the educational objectives of the urban and non-urban schools.

3) students at the fourth grade level have possibly experienced a more consistent educational program than those in the upper grades.

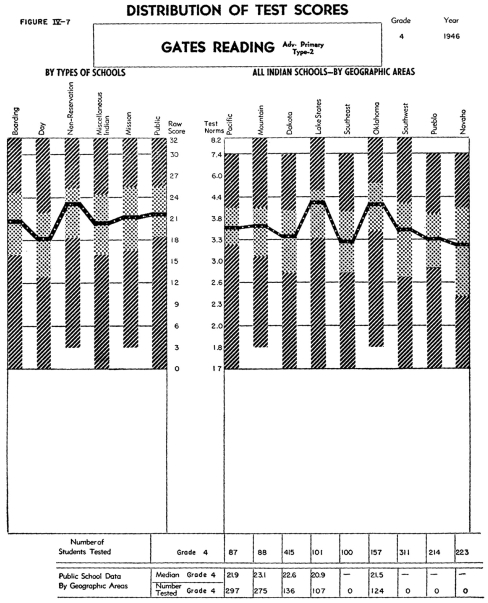
Figure IV-7 describes the achievement of the fourth grade students on the Gates Advanced Primary Reading, Type 2, which gives a measure of reading skill in interpreting the meaning of paragraphs. As in the preceding figure, these data also demonstrate that apparently the reading skills, as well as the vocabulary skills of the rural public and Indian schools are similar to those of urban students. Here, also, the rural public school students attain the achievement of the fourth grade city school pupils, whereas the Indian School students in the Lake States and Oklahoma areas exceed that level, and the reading of the non-reservation and miscellaneous Indian schools approximates that of the rural public students.

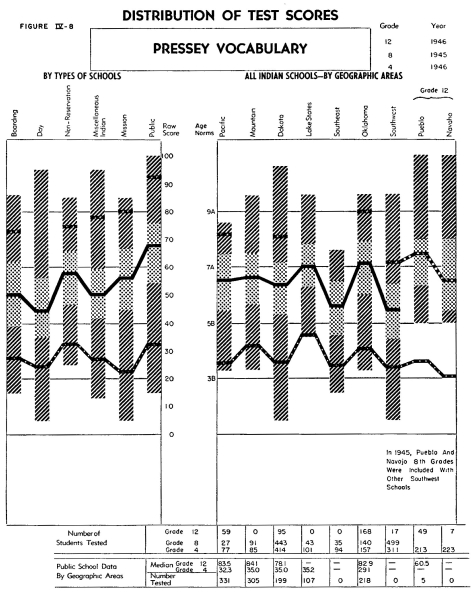
Figure IV-8 describes the achievement of the fourth, eighth and twelfth grade students on the Pressey Vocabulary Test. This substantiates the findings described in the preceding paragraph and shows that all of the fourth grade rural public schools and some types of Indian Schools tested achieve approximately fourth grade level on the national urban norms.

The Pressey Vocabulary Examination was given so as to add to the data obtained from the reading examinations. On the vocabulary examination the eighth grade rural public school children achieved the eighth grade level as estimated by national urban norms. It may be observed that, in general, the vocabulary level was comparatively higher than the reading level. This would imply that the difficulties encountered in reading certainly cannot be attributed alone to lack of word understanding. Instead, the reading difficulties encountered by the Indian students may be due to little opportunity to read, or to the fact that it was impossible to find reading tests at the upper grade levels in which the content of the passages was suited to rural populations.

Examinations such as the vocabulary test are usually prepared by surveying the words used or encountered by the group in question. This would mean that the Pressey Vocabulary test might not be the one best suited for measuring the working vocabulary of Indian students, for this test undoubtedly samples best the words encountered by urban students. Considering this limitation, it is surprising that the Indian students performed as well as they did on such a measuring instrument. Considerable thought was given to the construction of a special vocabulary examination designed for Indian students, using words and meanings out of their own experience and environment. A general vocabulary examination could not be constructed and administered in time for either the 1945 or 1946 battery. However, a special vocabulary test was constructed and included in the 1946 battery, whose special purpose was to determine if the vocabulary of certain tests could have accounted for low achievement in the tests. This will be discussed later.

Vocabulary growth for most of the types of schools and areas seems to be about the some for the four-year period between the fourth and eighth grades as it is between the eighth and twelfth grades. This means that, in general, the variations that are found between the schools and areas at one grade level are reflected in the school achievement at the higher grade levels. The growth in these two four-year periods is similar for almost all schools and areas. This may be interpreted to mean that the difference in achievement at the upper levels of achievement is probably due to some factor other than difference in school type. The only type of school in which the growth of vocabulary between the eighth and twelfth grades is not closely comparable to the growth between the fourth and eighth grades is in the rural public schools. This may be explained partly on the ground that the eighth grade students, already having achieved relatively high scores, find it difficult to demonstrate on this test their full increment of growth at the twelfth grade level. In other words, it is possible that this examination exerts a ceiling effect and does not allow accurate measurement at the twelfth grade levels. On the other hand, this difference might also be attributed to the fact that at the tenth, eleventh and twelfth grade levels the type of vocabulary learned by rural school children deviates further from that of urban students than it does at the fourth and eighth grades. A "ceiling effect" on this test is pointed to by the fact that in many of the schools and areas some twelfth grade students were able to answer all of the items on the test.

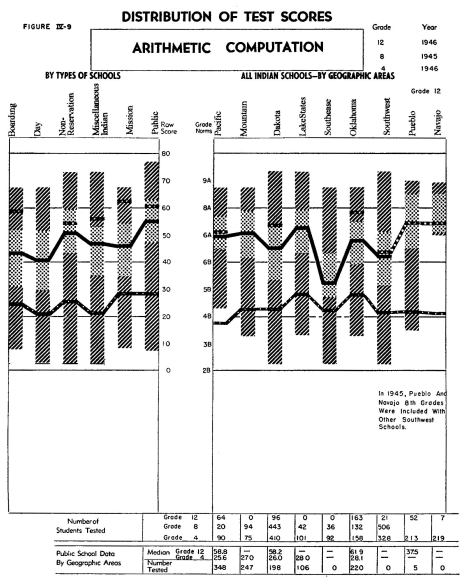
On the Arithmetic Computation test, which requires a number sense, but little or no reading of words and phrases, the students in all groups did comparatively well, as indicated by data in Figure IV-9. 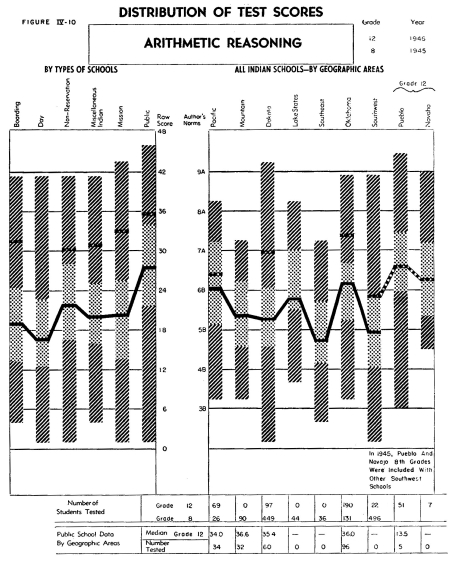While there were variations between groups, only one of the eighth grade groups had a median lower than Grade 5-A, and the medians of the eighth grade Indian groups were not more than one grade level below the median of the eighth grade rural public school students. The eighth grade medians on the Arithmetic Reasoning test plotted in Figure IV-10 are considerably lower than those on the Arithmetic Computation test. The reasoning test involves not only a number sense and skill in problem solving, but reading skill, which is in turn dependent upon the use of language and the understanding of certain experiences unfamiliar to many Indians. The range of eighth grade medians on the Arithmetic Reasoning test is from about Grade Equivalent 7-A to below 5-B, with the Indian groups, as a whole, considerably below the public school groups. At the twelfth grade level there is less difference between the achievement of the Indian groups and the public school group, indicating that the language factor appears to have been less of a handicap for these twelfth grade students than for the eighth grade students.

Inspection of Figure IV-9 discloses a much greater variability between the median achievements of the eighth grade students in the different schools and areas than between the- median achievement of the different fourth and twelfth grade groups. This is partly explained by the fact that, for the fourth grade groups, all were able to demonstrate to about the same degree their understanding of fundamentals, but it is impossible to account for the similarity between the twelfth grades on the basis of any ceiling effect when the twelfth grade students make scores no higher than they do. The relatively small difference between the achievement in the eighth grade and twelfth grade groups might be accounted for in some cases by the fact that, in this four-year interval, little attention is given to formal instruction in arithmetic fundamentals. It should be noted, however, that this lack of formal instruction should not give the schools a rationale for this low achievement on the part of the twelfth grade students, for, during this four-year interval, the teaching should include sufficient application of principles necessitating the use of these fundamentals so as to improve the students' use and understanding of them.

Analysis of the data in which the boarding, day and non-reservation schools in Oklahoma, Dakota, and the Southwest areas have been compared by the method of analysis of variance, indicates that the differences between these three types of schools, at the twelfth grade level, are probably no greater than that which could have occurred by chance, but differences as large, or larger than those occurring between these three areas could probably be interpreted as significant,* or in other words, not due to mere chance.

The Arithmetic examination is an excellent example by which to show the relatively high achievement of the Indian groups in Federal schools. In spite of the fact that much of the Indian student's time is devoted to special training for rural living and various trades, he has demonstrated a remarkably high level of performance in an academic subject such as Arithmetic Computation, in relation to those students in public schools, who presumably spend a larger per cent of the school day in instruction in the tool subjects. The fact that the Indian students do less well on the Arithmetic Reasoning Test than on the Arithmetic Computation gives added evidence that the lower level of reading ability is an important factor in measuring their achievement.

Figures IV-1 1, 12, 13 and 14 describe the data obtained from the administration of the Pressey English Examination. Here the students have been given four examinations in English which have yielded four separate scores. All parts of this test are of interest, because of the relatively small variations between the medians of the different eighth grade groups and the rather large range in increments between the eighth and twelfth grades.

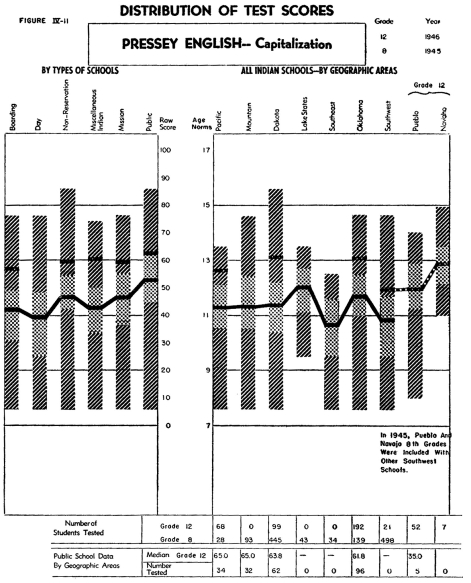
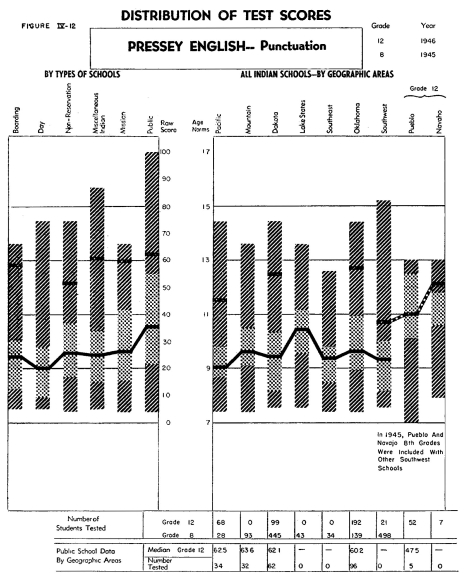
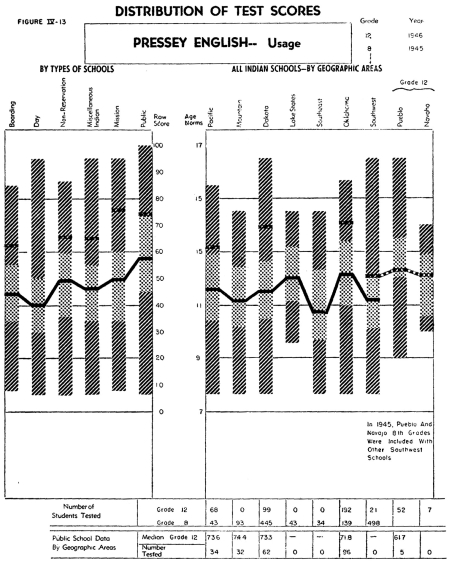
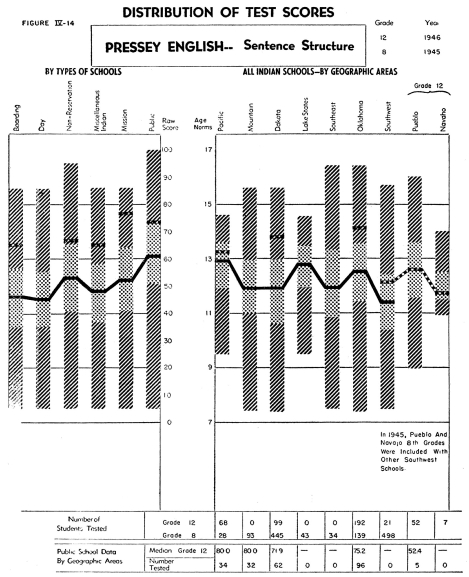
The four separate parts present an interesting profile on the students' ability to recognize different types of errors in English. In general, it may be concluded that the students included in this study probably do their best work on the recognition of errors in sentence structure and their poorest work in punctuation. As might be expected, in the Southwest, where the students' growth in the use of English is more dependent upon his formal school instruction than in areas where a larger per cent of the students come from English-speaking homes, the increment of growth between the eighth and twelfth graders is somewhat smaller than in the other areas.

The results on this examination must be interpreted differently from the results on the Free Writing Tests, described in the following chapter. The Pressey Test requires the students to demonstrate their competence in a wide range of situations, by establishing the situation, whereas the Free Writing examinations measure competence in a situation which the student himself establishes.

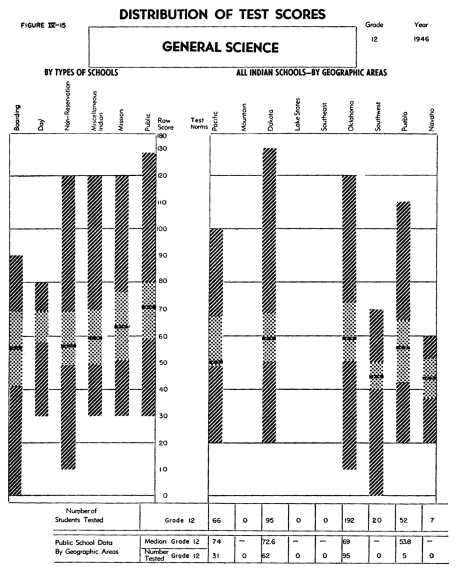
Figure IV-15 describes student performance on the United States Armed Forces Institute General Science Test. This test is composed of three sections: Part I - Basic Facts and Information; Part II - Application of Scientific Principles; and Part III - Scientific Attitudes and Application of the Scientific Method. The norms available on this examination are again based upon urban populations and for students whose courses of study have included from one to three years of specific training in general science. Analysis of the test results by its three parts indicates that the Indian students did very poorly on the last section, namely the application of scientific method. The relatively low scores on this part resulted largely from omissions and the fact that many students failed to complete this part of the test, rather than from an increased percentage of error on the items which were attempted. Most of the students did fairly well on the first two parts-in fact, had they performed as well on the third part as they did on the first two parts, their standing would have been nearly equal to that on the tentative national norms. While no data are available to indicate the amount of specific training included in the courses of study of the rural public schools, it will be noted that they achieved the level established by the tentative urban norms.

* Data indicates that differences this large could occur by chance fewer than five times in one-hundred.